参数估计

在概率统计或者数据挖掘的各种模型中，我们经常会遇到各种参数估计的问题。本文主要通过两个例子来介绍参数估计的常用方法。 例子1：设总体 $X$ 的均值 $\mu$ 和方差 $\sigma^2$均未知, 已知$X_1, X_2, \ldots, X_n$ 是一个样本, 估计均值 $\mu$ 和方差 $\sigma^2$。 例子2：抛一枚硬币，正面朝上的概率为 $\theta$，已知一共抛了20次，其中12次朝上，8次朝下。问抛第21次的时候，硬币应该是朝上还是朝下？

---

1 点估计

设总体X的分布函数形式已知，但有一个或者多个未知参数，借助于总体X的一个样本来估计总体未知参数的值的问题称为参数的点估计问题。点估计实际上代表了频率学派的观点，频率学派认为参数是客观存在的，只是我们不知道罢了。只要参数求出来了，给定一个 $X$ ，相应的 $y$ 也就确定了。常用的点估计方法有矩估计法、最大似然估计法和最大后验估计。

1.1 矩估计

分别计算样本矩和总体矩的前k阶矩，利用样本矩依概率收敛于总体矩的性质，构造相应的方程组，用方程组的解作为参数的估计量，这时候的估计量称为矩估计量。 用矩估计法解上面的例子1，易知总体矩：

$$\begin{equation} \begin{split} \mu_1 &= E(X) = \mu \\ \mu_2 &= E(X^2) = D(X) + [E(X)]^2 = \mu^2 + \sigma^2 \end{split} \end{equation}$$

计算样本矩：

$$\begin{equation} \begin{split} A_1 &= \frac {1}{n} \sum_{i=1}{ X_i = \overline {X } }\\ A_2 &= \frac {1}{n} \sum_{i=1}^n X_i^2 \end{split} \end{equation}$$

联立方程组：

$$\begin{equation} A_1 = \mu_1, A_2 = \mu_2 \end{equation}$$

解得：

$$\begin{equation} \begin{split} \hat{\mu} &= \overline {X} \\ \hat {\sigma^2} &= \frac {1}{n} \sum_{i=1}^{n}(X_i - \overline {X})^2 \end{split} \end{equation}$$

1.2 最大似然估计（Maximum Likelihood Estimation）

在讲最大似然（ML）估计之前，我们先来回顾一下贝叶斯公式：

$$\begin{equation} p(\theta | X) = \frac {p(X | \theta) \cdot p(\theta)}{p(X)} \end{equation}$$

这个公式用对应的术语来表示的话：

$$\begin{equation} posterior = \frac {likelihood \cdot prior}{evidence} \end{equation}$$

设总体$X$属于离散性，其分布律为 $P(X=x)=p(x | \theta)$，形式已知，但参数$\theta$未知。已知$X_1, X_2, \ldots, X_n$ 是一个样本，则$X_1, X_2, \ldots, X_n$的联合分布律为:

$$\begin{equation} \Pi_{i=1}^{n}p(x_i | \theta) \end{equation}$$

设$x_1, x_2, \ldots, x_n$是相应于样本$X_1, X_2, \ldots, X_n$的一个样本值，已知样本取到$x_1, x_2, \ldots, x_n$的概率，也即事件 ${ X_1=x_1, X_2 = x_2, \ldots, X_n = x_n}$ 发生的概率为：

$$\begin{equation} \begin{split} L(\theta | X) &= p(x_1, x_2, \ldots, x_n |\theta) \\ & = \Pi_{i=1}^{n}p(x_i|\theta) \end{split} \end{equation}$$

这一概率随 $\theta$的变化而变化，是$\theta$的函数，称为样本的似然函数。用似然函数取得最大值的$\theta$作为原分布律未知参数的估计值，称为极大似然估计值。求解的时候一般会把这个似然函数取对数，转化成求和的形式。

$$\begin{equation} \begin{split} \hat { \theta_{ML} } &= argmax_{\theta} L(\theta | X) & = argmax_{\theta} \sum_{X} \log p(X|\theta) \end{split} \end{equation}$$

当总体$X$属于连续型时，考虑的是样本$X_1, X_2, \ldots, X_n$ 落到$x_1, x_2, \ldots, x_n$ 的领域内的概率，和离散性的表达形式一样。用最大似然估计解上面的例子1：

$X$的概率密度为：

$$\begin{equation} f(x | \mu, \sigma^2) = \frac {1}{\sqrt {2 \pi \sigma^2}} e^{-\frac {(x-\mu)^2}{2 \sigma^2}} \end{equation}$$

似然函数为：

$$\begin{equation} L(\mu, \sigma^2)=\Pi_{i=1}^{n} \frac {1}{\sqrt {2 \pi \sigma^2}} e^{-\frac {(x-\mu)^2}{2 \sigma^2}} \end{equation}$$

取对数，然后分别对 $\mu$，$\sigma^2$求偏导数，并令偏导数为0，解得：

$$\begin{equation} \begin{split} \hat{\mu} &= \overline {X} \\ \hat {\sigma^2} &= \frac {1}{n} \sum_{i=1}^{n}(X_i - \overline {X})^2 \end{split} \end{equation}$$

可以看出，对例子1，用最大似然估计和用矩估计法求得的估计值完全相同。 对例子2，每一次抛硬币的事件 $X_i$，都得到硬币朝上或者朝下的结果 $x_i \in {0, 1} $, 其中1表示正面朝上，0表示正面朝下。

$$\begin{equation} \begin{split} L &= \log \Pi_{i=1}^{N} p(X_i=x_i | \theta) \\ & = \sum_{i=1}^{N} \log (X_i=x_i | \theta) \\ & = n^{(1)} \log p(X_i=1 | \theta) + n^{(0)} \log p(X_j=0 | \theta) \\ & = n^{(1)} \log \theta + n^{(0)} \log (1-\theta) \\ \end{split} \end{equation}$$

其中 $n^{(1)}$ 表示正面朝上的次数，$n^{(0)}$ 表示正面朝下的次数。上式对 $\theta$求导并令其等于0得到：

$$\begin{equation} \begin{split} \frac {\partial L} {\partial \theta} &= \frac {n^{(1)}} {\theta} - \frac {n^{(0)}} {1-\theta} = 0 \\ \theta &= { n^{(1)} \over {n^{(1)} + n^{(0)}} } = {12 \over 20} = 0.6 \end{split} \end{equation}$$

1.3 最大后验估计（Maximum a Posteriori Estimation）

最大后验估计（MAP）也是点估计的一种方法，跟最大似然估计很相似，此时不是要求似然函数最大，而是要求要求后验概率最大。

$$\begin{equation} \begin{split} \hat {\theta_{MAP}} &= argmax_{\theta}{ p(X | \theta)p(\theta) \over p(X)} \\ & = argmax_{\theta} p(X | \theta)p(\theta) \\ & = argmax_{\theta} {L(\theta | X) + \log p(\theta)} \\ & = argmax_{\theta} {\sum_X \log(p(x|\theta)) + \log p(\theta) } \end{split} \end{equation}$$

可以看出最大后验估计不同于最大似然估计的是在估计参数 $\theta$ 时引入了一个先验概率。这个先验概率在实际应用中往往指人们已经接受的普遍规律。比如抛硬币的实验，如果抛了3次硬币，每次都是正面朝下，按照最大似然估计就会得出硬币正面朝上的概率为0这一结论，这显然与人们的常识相违背。人们已经认知的规律是一个公平的硬币，正面朝上的概率一般是0.5，也就是说硬币正面朝上的概率分布会在0.5处取得最大值，这个概率分布就是先验分布。假设先验分布的参数是 $\alpha, \beta$，即先验分布表示为：$p(\theta) = p(\theta | \alpha, \beta)$。

一般先验会选择似然函数的共轭先验，这样计算出来的后验概率和先验概率就是共轭分布，有关共轭分布的只是请参考 PRML 第二章[3]。这里我们选取 beta 分布作为 $\theta$ 的先验分布，令超参数 $\alpha = \beta = 5$：

$$\begin{equation} \begin{split} p(\theta | \alpha, \beta) &= Beta(\theta | \alpha, \beta) \\ & = {1 \over B(\alpha, \beta)} \theta^{\alpha -1} (1-\theta)^{\beta -1} \end{split} \end{equation}$$

将这个式子带入（15）式，对 $\theta$ 求导，令导数为0：

$$\begin{equation} \begin{split} {\partial \hat {\theta_{MAP}} \over \partial \theta} &= {n^{(1)} \over \theta} - {n^{(0)} \over 1-\theta} + {\alpha -1 \over \theta} -{\beta -1 \over 1-\theta} \\ & = 0 \end{split} \end{equation}$$

求解得到：

$$\begin{equation} \begin{split} \hat {\theta_{MAP}} &= \frac {n^{(1)} + \alpha -1 }{ n^{(1)} + n^{(0)} + \alpha + \beta -2 } \\ & = \frac {n^{(1)} + 4}{n^{(1)} + n^{(0)} + 8} \\ & = \frac {16} {28} \\ & = 0.571 \end{split} \end{equation}$$

比最大似然估计得出来得0.6更接近0.5，也就是更接近硬币两面公平这一事实。

2 贝叶斯估计

贝叶斯估计和最大似然估计、最大后验估计不一样，属于贝叶斯学派的观点，这个学派认为待估计的参数也是一个随机变量，当给定一个输入 $X$ 后，我们不能用一个确定的 $y$ 来表示输出，必须用一个概率的方式表达出来，所以贝叶斯预测的是一个期望值。贝叶斯估计跟最大后验估计不一样的地方是不直接估计参数的值，而是求出参数的概率分布，然后求这个概率分布的期望。

$$\begin{equation} \begin{split} p(\theta | X, \alpha, \beta) &= \frac { \Pi_{i=1}^N p(X_i = x_i | \theta) p(\theta | \alpha, \beta) } { \sum_{\theta} \Pi_{i=1}^N p(X_i = x_i | \theta) p(\theta | \alpha, \beta) } \\ & = \frac {\theta ^ {n^{(1)}} (1-\theta)^{n^{(0)}} {1 \over B(\alpha, \beta)} \theta ^ {\alpha -1} (1-\theta)^{\beta -1} } {Z} \\ & = \frac { \theta ^{ n^{(1)} + \alpha -1 } (1-\theta)^{n^{(0)} + \beta -1} } {B(n^{(1)}+\alpha, n^{(0)}+\beta)} \\ & = Beta(\theta | n^{(1)}+\alpha, n^{(0) + \beta}) \end{split} \end{equation}$$

然后根据上式求出 $\theta$ 的期望即可：

$$\begin{equation} \begin{split} \hat {\theta_{Bayes}} &= E(\theta) \\ & = \frac {n^{(1)} + \alpha} {n^{(1)} + n^{(0)} + \alpha + \beta} \\ & = \frac {17} {30} \\ & = 0.567 \end{split} \end{equation}$$

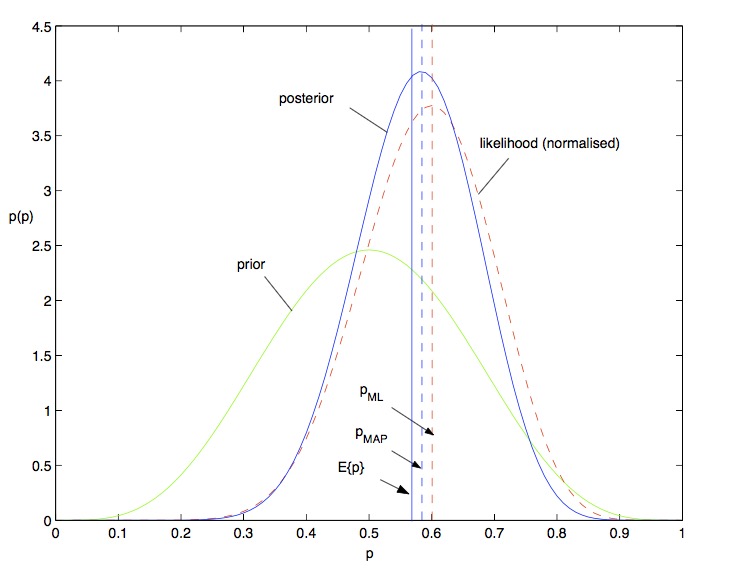
可以看出贝叶斯估计得出来的值比最大后验估计又更接近了0.5，如下图所示[2]：

3 估计量的评选标准

评价一个估计量的好坏，有很多常用的标准，这里只介绍最常用的两个标准，无偏性和有效性。

3.1 无偏性

如果估计量$\hat {\theta}=\hat {\theta}(X_1, X_2, \ldots, X_n)$的期望存在，而且有：

$$\begin{equation} E(\hat{\theta}) = \theta \end{equation}$$

则称$\hat {\theta}$为$\theta$的无偏估计量。

检验上面例子1用最大似然估计得到的估计值：

$$\begin{equation} E(\hat {\sigma^2}) = \frac {n-1}{n} \sigma^2 \neq \sigma^2 \end{equation}$$

所以估计量$\hat {\theta}$是有偏的。

3.2 有效性

设估计量$\hat {\theta_1}=\hat {\theta_1}(X_1, X_2, \ldots, X_n)$和估计量$\hat {\theta_2}=\hat {\theta_2}(X_1, X_2, \ldots, X_n)$都是$\theta$的无偏估计量，如果：

$$\begin{equation} D(\hat {\theta_1}) < D(\hat {\theta_2}) \end{equation}$$

则称 $\hat {\theta_1} $比$\hat {\theta_2} $有效。

4 参考资料

1. 概率论与数理统计 高等教育出版社
2. http://www.arbylon.net/publications/text-est.pdf
3. Pattern Recognition and Machine Learning Chapter2

---