推荐系统

推荐系统是近几年比较火的一个话题, 尤其是Netflix举办过一次电影推荐比赛之后, ACM有专门的Recommer System的会议. 关于推荐系统的分类, 从不同的角度有不同的分法, 传统的有两种分法, 一种叫基于内容(Content based)的推荐, 顾名思义就是根据要推荐的项目(电影, 书籍, 音乐等等)本身的一些DNA进行推荐, 比如电影的类型, 是动作片还是爱情片还是动作爱情片? 电影的导演是否有名, 演员的阵容怎么样等等. 还有一种叫协同过滤(Collaborative Filtering), 协同过滤按照算法又可以分成很多小类, User-based, Item-based, Slope-one, Model-based, 下面就以一个实际例子来介绍不同的推荐算法是怎么实现的.

例子: 假设我们获取了一些用户在对一些项目的评分, 我们的目的是预测某个用户对某个项目的评分. 如下面的表格所示, 我们拿预测User1对Item2的评分举例.

	Item1	Item2	Item3	Item4
User1	4	?	5	5
User2	4	2	1
User3	3		2	4
User4	4	4
User5	2	1	3	5

1 基于内容(Content Based)的推荐

Content-based是说我们在已经知道了Item DNA的情况下, 基于这些DNA去做推荐. 比如我们的Item是电影, 那Item的DNA可能是电影的类型, 我们拿喜剧片, 爱情片和科幻片举例. 假如Item 2 是一部喜剧片, 同时也可以是一部爱情片, 我们用一个三维向量表示为:

$\mathbf{x}^2 = (1, 0.99, 0)^T$

如果同时我们也知道了用户喜欢什么样的电影, 到底是喜欢喜剧片多一点还是喜欢科幻片片多一点? 那么用户的喜好也可以用一个三维向量来表示, 假如用户1只喜欢爱情片(喜好程度用0-5来表示), 那么用户1的爱好用向量表示为:

$\mathbf{w}^1=(0, 5, 0)^T$

那么, 我们基于这两个向量就可以预测用户1会给Item 2 评多少分:

$r^{1, 2} = {\mathbf{w}^1}^T \cdot \mathbf{x}^2 = 0 \times 1 + 5 \times 0.99 + 0 \times 0 = 4.95$

但实际上我们并不知道表征喜好程度的向量, 我们的目的是要学习出这个向量. 为此, 我们想定义一些符号:

$n_u$ : 表示一共有多少用户
$n_m$ : 表示一共有多少Item
$c(i, j)$ : =1表示用户 i 评价过 Item j
$r^{i, j}$ : 表示用户 i 对 Item j 的评分
$\mathbf{x}^j$ : 表征 Item j 的特征向量
$\mathbf{w}^i$ : 表征用户的特征向量(未知, 需要学习)
$m^i$ : 用户 i 评价过的 Item 数量
$n+1$ : $\mathbf{x}$ 和 $\mathbf{w}$ 的维度

为了学习到用户的特征向量, 我们需要定义一个学习策略, 我们仍然采用先定义损失函数, 然后对损失函数求极小的策略来学习用户特征. 很自然的一个选择就是采用平方损失函数. 用户 i 对 Item j 的评分损失(误差)为:

$( {\mathbf{w}^i}^T \cdot \mathbf{x}^j - r^{i, j} )^2$

对某个用户 i 来说, 损失为:

$\frac {1} {2m^i} \sum_{j : c(i, j)=1} ( {\mathbf{w}^i}^T \cdot \mathbf{x}^j - r^{i, j} )^2 + \frac {\lambda}{2m^i} \sum_{k=1}^{n} (w_k^i)^2$

对所有的用户来说, 损失为:

$L(\mathbf{w}) = \frac {1}{2} \sum_{i=1}^{n_u} \sum_{j : c(i, j)=1} ({\mathbf{w}^i}^T \cdot \mathbf{x}^j - r^{i, j})^2 + \frac {\lambda}{2}\sum_{i=1}^{n_u}\sum_{k=1}^{n}(w_k^i)^2$

最小化上面的损失函数, 采用梯度下降进行迭代:

$w_k^i : = w_k^i - \alpha \sum_{j : c(i, j)=1} ( {\mathbf{w}^i}^T \cdot \mathbf{x}^j - r^{i, j} ) x_k^j \qquad (for \qquad k=0)$ $w_k^i : = w_k^i - \alpha (\sum_{j : c(i, j)=1} ( {\mathbf{w}^i}^T \cdot \mathbf{x}^j - r^{i, j} ) x_k^j + \lambda w_k^i) \qquad (for \qquad k \neq 0)$

2 协同过滤(Collaborative Filtering)

2.1 Item-based

如下图所示, 我们有三个用户1, 2, 3和三个电影A, B, C. 用户1喜欢电影A和电影C, 用户2喜欢电影A, B, C, 用户3喜欢电影A. 假设电影A和电影C很相似(这里的相似性不是由A和C本身的DNA得到的, 至于计算方面后面再说), 那么我们有理由预测用户3会喜欢电影C, 因为她喜欢A, 而A和C很相似.

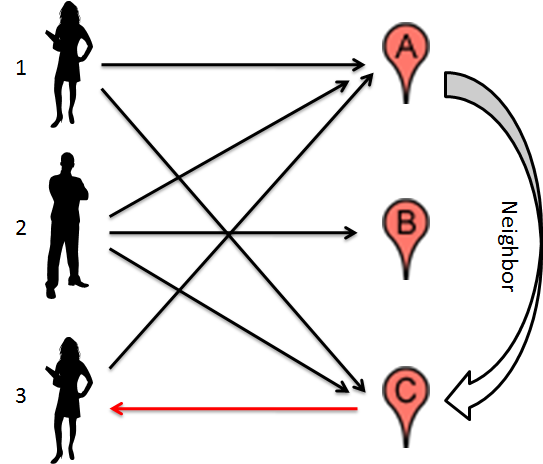
Item-based

如果用户1给电影A打了5分, 而A和C又有90%的相似, 那么我们会预测说用户3给电影C的评分是 $5 \times 0.9=4.5$ 分. 这就是所谓的Item-based. 推广一下, 回头看看我们开头的例子, 我们的任务是要预测用户1会给Item2评多少分, 如果我们已经知道了Item2和Item1, Item2和Item3, Item2和Item4之间的相似性, 那么我们预测:

$p^{u1, i2} = \frac {r^{u1, i1}s^{i2, i1} + r^{u1, 31}s^{i2, i3} + r^{u1, i4}s^{i2, i4}} {s^{i2, i1}+s^{i2, i3}+s^{i2, i4}}$

那么问题来了, 在不知道Item本身的信息的情况下, 如何计算两个Item之间的相似性呢? 如果我们把每个Item都用一个列向量来表示, 其中向量里的每一维都是不同的用户对这个Item的评分, 那么计算两个Item之间的相似性就转化成我们熟悉的计算两个向量之间的相似性了, 可以采用余弦距离(Cosine distance), 皮尔逊相关性系数(Peason correlation coefficient), 杰卡德相似系数(Jaccard similarity coefficient)等等. 这里我们拿皮尔逊相关性系数举例:

$s^{i, j}=\frac {\sum_{u \in U} (r^{u, i} - \overline{r^i}) (r^{u, j} - \overline{r^j}) } {\sqrt{ \sum_{u \in U} (r^{u, i} - \overline{r^i})^2 } \sqrt{ \sum_{u \in U} (r^{u, j} - \overline{r^j})^2 } }$

其中:

$s^{i, j}$ 表示Item i 和Item j之间的相似性
$U$ 表示同时评价过Item i和Item j的用户集合
$\overline{r^i}$ 表示用户集合 $U$ 在Item i上的平均评分
$\overline{r^j}$ 表示用户集合 $U$ 在Item j上的平均评分

用户 a 对 Item i 的评分预测公式为:

$p^{u, i} = \frac {\sum_{j \in I} r^{u, j}s^{i, j}}{\sum_{j \in I} |s^{i, j}|}$

其中: $I$ 为用户 a 评价过的Item集合

那么预测User 1 对 Item 2 评分的具体计算步骤为:

找出User 1 评价过的Item集合: Item 1, Item3, Item 4

计算Item 2 和Item 1, Item 3, Item 4之间的相似度

找出同时评价过 Item 2 和 Item 1的用户集合U: 用户2, 用户4和用户5

用户集合U在 Item 1 上的平均分3. 33, 在Item 2 上的平均分2. 33, 所以: $s^{2, 1} = \frac {0. 67 \times -0. 33 + 0. 67 \times 1. 67+ -1. 33 \times -1. 33} {\sqrt {0. 67^2 + 0. 67^2 + (-1. 33)^2} \sqrt {0. 33^2 +1. 67^2 + 1. 33^2}} = 0. 754$

同理, 计算出 $s^{2, 3}=-1, s^{2, 4}=0. 756$

根据相似度和评分预测公式计算出预测分数 $p^{1, 2} = \frac {4 \times 0. 754 + 5 \times (-1) + 5 \times 0. 756} {0. 754 + 1 + 0. 756} = 0. 716$

在实际工程中, 我们遇到的Item数量往往很大, 如果在线去计算所有 Item 两两之间的相似度的话肯定不现实, 那么实际工程中应该怎么处理呢? 这里提供两个方法:

方法一: 对所有Item进行预处理, 一般是用哈希的思想, 将可能相似的Item集合Hash到一个桶里, 那么在线计算的时候, 只需要计算在某个桶里的Item两两之间的相似性了, 具体做法请google LSH, 这里不多说.
方法二: 用分布式计算离线把所有Item 之间的相似性都计算好, 在线直接查询就行.

还是以上面的例子来介绍怎么用map-reduce的框架来计算item之间的相似性, 整个计算过程采用两个map-reduce过程.

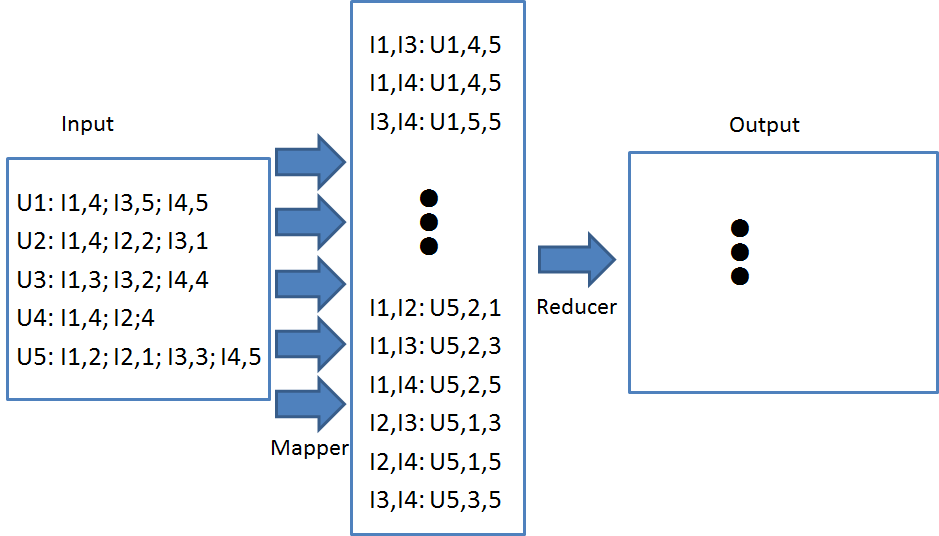
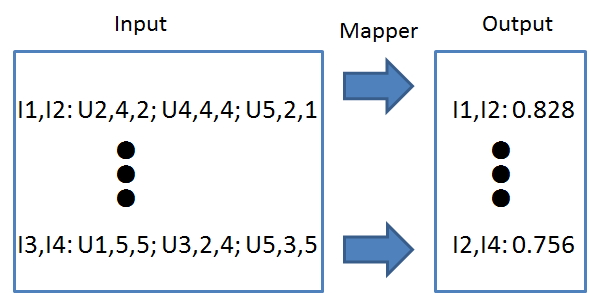
2.2 User-based

如下图所示, 我们有三个用户1, 2, 3和四个电影A, B, C, D. 用户1喜欢电影A和电影C, 用户2喜欢电影B, 用户3喜欢电影A, 电影C和电影D. 如果用户1和用户3很相似(同样, 相似性也不是基于用户本身的DNA来计算的, 后来再介绍), 那么我们有理由预测用户1会喜欢电影D, 因为用户1喜欢电影A和C, 用户3喜欢电影A, C和D, 而用户1和用户3又比较相似. 这就是所谓的User-based.

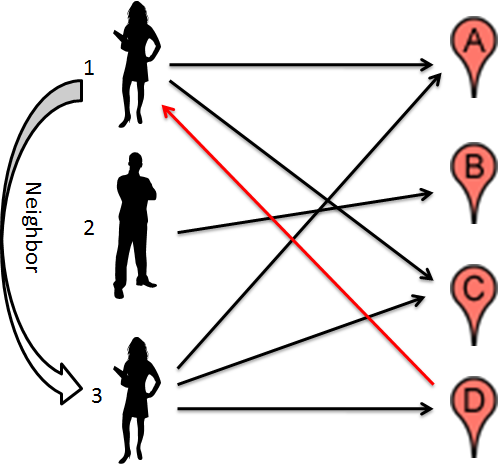
那么我们用这种算法怎么预测用户1对Item 2的评分呢? 跟Item-based类似, 我们先看看怎么计算两个用户之间的相似性:

$s^{u, v}=\frac {\sum_{i \in I} (r^{u, i} - \overline{r^u}) (r^{v, i} - \overline{r^v}) } {\sqrt{ \sum_{i \in I} (r^{u, i} - \overline{r^u})^2 } \sqrt{ \sum_{i \in I} (r^{v, i} - \overline{r^v})^2 } }$

其中:

$I$ 为用户u, 用户v同时评价过的Item集合
$\overline{r^u}$ 为用户 u 对 I 里所有 Item 评分的平均值
$\overline{r^v}$ 为用户 v 对 I 里所有 Item 评分的平均值

User-based的评分的预测公式与Item-based的评分预测公式稍微有点不一样:

$p^{a, i} = \overline{r^a} + \frac {\sum_{u \in U} (r^{u, i} - \overline{r^u}) s^{a, u}} {\sum_{u \in U} |s^{a, u}|}$

其中:

$U$ 为所有评价过Item i 的用户集合
$\overline{r^a}$ 为用户 a 对所有他评价过的Item的评分的平均值
$\overline{r^u}$ 为用户 u 对所有他评价过的Item的评分的平均值(Item i 除外)

为什么User-based和Item-based的评分预测公式会有区别呢? 主要是为了消除用户评分的bias, 有的用户就是喜欢评低分, 而有的用户习惯给高分. 那么, 预测用户1在Item 2 上的评分的步骤为:

找出评价过Item 2 的用户集合: 用户2, 用户4和用户5

计算用户1和用户2, 用户4, 用户5之间的相似性

找出用户1和用户5同时评价过的Item 集合I: Item 1, Item 3 和 Item 4

用户1在 I 上的平均分为4. 67, 用户5在I上的平均分为3. 33, 所以: $s^{1, 5} = \frac {-0. 67 \times -1. 33 + 0. 33 \times 0. 33 + 0. 33 \times 1. 67}{\sqrt {(-0. 67)^2 + 0. 33^2 + 0. 33^2} \sqrt {(-1. 33)^2 + 0. 33^2 + 1. 67^2}} = 0. 756$

同理计算 $s^{1, 2}=-1, s^{1, 4}=0$

根据相似性和评分预测公式计算预测分 $p^{1, 2} = 4. 67 + \frac {(2-2. 5) \times (-1) + (4-4) \times 0 + (1-3. 33) \times 0. 756}{1+0+0. 756} = 3. 95$

2.3 Slope-one

Slope-one基于一种简单的假设, 假设任意两个Item i 和 j 之间的评分存在某种线性关系, 即知道了Item j 的评分, 我们可以用线性公式来预测 Item i 的评分, $p^{u, i}= a r^{u, j}+b^{u, i, j}$ , 更进一步的假设斜率 $a=1$ , 这就是算法为什么叫Slope-one的原因. 为了求得b, 我们先定义一个平方损失函数:

$L(b^{i, j}) = \sum_{u \in U}(r^{u, i} - p^{u, i})^2 = \sum_{u \in U}(r^{u, i} - r^{u, j} - b)^2$

其中: $U$ 是同时评价过Item i 和 Item j 的用户集合.

最小化上面的损失函数得到:

$b^{i, j} = \frac {\sum_{u \in U}(r^{u, i} - r^{u, j})} {\sum_{u \in U} 1}$

预测用户a对Item i 的评分预测公式为:

$p^{a, i} = \frac {\sum_{j \in I}(r^{a, j} + b^{i, j})} {\sum_{j \in I} 1}$

那么用Slope-one预测用户1在Item 2 上的评分步骤为:

找到同时评价过Item 1 和Item 2的用户: 用户2, 用户4和用户5

计算Item 2 和 Item 1 的平均分差 $b^{2, 1} = \frac {(2-4) + (4-4) +(1-2)} {3} = -1$

仿照步骤1和步骤2计算 $b^{2, 3} =-0. 5, b^{2, 4}=-4$

按照预测公式计算预测分 $p^{1, 2} = \frac {(4-1) + (5-0. 5) + (5-4)} {3} = 2. 83$

2.4 Weighted Slope-one

后来又演变出一种叫Weighted Slope-one的算法, 它的思想和Slope-one一样, 只是最后的评分预测公式加入了权重.

$p^{a, i} = \frac {\sum_{j \in I}(r^{a, j} + b^{i, j})c^{i, j}} {\sum_{j \in I} c^{i, j}}$

我们在上面计算 $b^{2, 1}$ 的时候, 是根据三个用户的共同评分计算出来的, 而在计算 $b^{2, 3}$ 的时候, 是根据两个用户的共同评分计算出来的, 计算 $b^{2, 4}$ 的时候只根据了一个用户的评分. 所以他们的权重分别是 $c^{2, 1}=3, c^{2, 3}=2, c^{2, 4}=1$ , 所以:

$p^{1, 2} = \frac {(4-1) \times 3 + (5-0. 5) \times 2 + (5-4) \times 1} {3+2+1} = 3. 17$

Item-based, User-based, Slope-one都各有优缺点. Item-based跟当前用户的行为相关, 比如在浏览一部动作片的时候, 推荐的结果可能就是另一部动作片, 但在浏览一部爱情片的时候, 推荐的结果可能就是一部爱情片. User-based考虑的相同爱好的用户群的兴趣, 推荐这个用户群喜欢过的某个Item, 与当前用户的行为关系不大, 比如在浏览一部动作片或者爱情片的时候, 推荐出来的结果可能都一样. Slope-one主要是计算起来比较方便, 也可以增量计算, 实现很简单.

思考一下: 新闻推荐用User-based还是Item-based好?

另外, 推荐的可解释性也是现在推荐系统非常强调的, 比如你在浏览Amazon的时候, 它的推荐都会给出“Why Recommended”的理由. Item-based和Content-based类似, 能给出很好的解释, 推荐的东西跟你现在浏览的东西相关, 因为你在看Java编程思想, 所以给你推荐Java相关的书籍. User-based的解释是说跟你趣味相投的某某也喜欢这个电影, 但是你可能并不认识这个某某, 所以很难让人信服. Slope-one就更没法给出合理的解释了.

2.5 Model-based

推荐问题其实也可以归结为机器学习里面的一个领域, 很自然的机器学习里常用的一些模型都可以应用到推荐系统里, 比如贝叶斯模型, 回归模型或者非常流行的矩阵分解, 都可以用来解决推荐问题, 这种自己建模或者用常用的模型去解决推荐问题的办法就叫Model-based. 这里我主要说两种Model-based, 一种是矩阵分解, 其实可以算真正意义上的协同过滤, 另一种就是著名的SVD++.

3 矩阵分解

前面在讲到 Content-based 推荐的时候说到, 如果我们知道了 Item 的特征向量, 就可以计算出用户的特征向量. 一模一样的道理, 如果我们知道了用户的特征向量, 就可以求出 Item 的特征向量, 那么我们的损失函数为:

$L(\mathbf{x}) = \frac {1}{2} \sum_{j=1}^{n_m} \sum_{j : c(i, j)=1} ({\mathbf{w}^i}^T \cdot \mathbf{x}^j - r^{i, j})^2 + \frac {\lambda}{2}\sum_{j=1}^{n_m}\sum_{k=1}^{n}(x_k^j)^2$

如果我们既不知道 Item 的特征向量, 又不知道用户的特征向量呢? 这时候我们就可以考虑先随便给一些 Random 的 Item 特征向量和用户的特征向量, 不断迭代上面所说的“由Item特征向量计算用户特征向量, 由用户特征向量计算Item特征向量”的过程. 最后我们还是一样用 ${\mathbf{w}^i}^T \cdot \mathbf{x}^j$ 来预测用户 i 对 Item j 的评分, 最后我们的整个评分预测矩阵会变为:

$\left[ \begin{matrix} {\mathbf{w}^1}^T \cdot \mathbf{x}^1 & {\mathbf{w}^1}^T \cdot \mathbf{x}^2 & \ldots & {\mathbf{w}^1}^T \cdot \mathbf{x}^{n_m}\\ {\mathbf{w}^2}^T \cdot \mathbf{x}^1 & {\mathbf{w}^2}^T \cdot \mathbf{x}^2 & \ldots & {\mathbf{w}^2}^T \cdot \mathbf{x}^{n_m} \\ \vdots & \vdots & & \vdots \\ {\mathbf{w}^{n_u}}^T \cdot \mathbf{x}^1 & {\mathbf{w}^{n_u}}^T \cdot \mathbf{x}^2 & \ldots & {\mathbf{w}^{n_u}}^T \cdot \mathbf{x}^{n_m} \end{matrix} \right]$

最后我们的损失函数就会变成:

$L(\mathbf{x}, \mathbf(w)) = \frac {1}{2} \sum_{(i, j) : c(i, j)=1} ({\mathbf{w}^i}^T \cdot \mathbf{x}^j - r^{i, j})^2 + \frac {\lambda}{2}\sum_{j=1}^{n_m}\sum_{k=1}^{n}(x_k^j)^2 + \frac {\lambda}{2}\sum_{i=1}^{n_u}\sum_{k=1}^{n}(w_k^i)^2$

同样我们采用梯度下降来解这个问题:

将 $\mathbf{x}, \mathbf{w}$ 初始化为一些Random的值

梯度下降迭代: $x_k^j : = x_k^j - \alpha (\sum_{i: c(i, j)=1} ({\mathbf{w}^i}^T \cdot \mathbf{x}^j - r^{i, j}) \mathbf{w}^i + \lambda x_k^j )$ $w_k^i : = w_k^i - \alpha (\sum_{j: c(i, j)=1} ({\mathbf{w}^i}^T \cdot \mathbf{x}^j - r^{i, j}) \mathbf{x}^j+ \lambda w_k^i)$

再回头看看那个评分预测矩阵, 是不是把原始矩阵分解成了两个矩阵的乘积, 是不是一个矩阵分解的问题? 我们在矩阵分解之前一般会做一些的Normalization的工作, 比如会把每个分数都减去该 Item 的平均分值. 最后再预测分数的时候把该平均值加回来即可. 我们有了所有 Item 的特征向量之后, 也可以很轻松的计算出任意两个 Item 之间的相似度了. 分解出来的两个矩阵一个表示了 User 特征, 一个表示了Item 的特征, 这种模型也可以叫做Latent Factor Model.

4 SVD++

SVD++ 实际上也是一种Latent Factor Model, 只不过做了一些改进. 首先假设一个用户对一个Item的评分由三部分组成:

$b^{i,j} = \mu + b^i + b^j$

其中:

$\mu$ 是所有用户对所有Item的评分的平均值.
$b^i$ 是用户i评分的bias.
$b^j$ 是Item j 的评分的bias.

举个例子: 假如我们要预测Joe对电影泰坦尼克号的评分. 假设整个评分数据集上的平均评分为3.7分, 也就是 $\mu=3.7$ . 而因为泰坦尼克号是一部高质量的电影, 所以用户对它的评分普遍会高一点, 假设会比平均分高0.5分, 也就是 $b^j=0.5$ . 但Joe是一个非常高品位的用户, 只有她遇到非常高质量的电影时, 她的评分才会比较高, 也就是说她的所有评分相对来说是比较偏低的, 假设偏低0.3分, 也就是 $b^i=-0.3$ , 那么我们预测Joe对泰坦尼克号的评分为:

$b^{i,j} = 3.7 - 0.3 + 0.5 = 3.9$

但实际上 $b^i$ 和 $b^j$ 我们是不知道的, 不过我们可以通过最小化下面的式子很快求出这两个值.

$\sum_{(i, j) : c(i, j)=1}( r^{i,j} - \mu - b^i - b^j )^2 + \lambda ({b^i}^2 + {b^j}^2)$

SVD++把上面的方法和矩阵分解的思想融合在了一起, 用户i对Item j 的评分预测为:

$p^{i,j} = b^{i,j} + {\mathbf{w}^i}^T \mathbf{x}^j = \mu + b^i + b^j + {\mathbf{w}^i}^T \mathbf{x}^j$

这时候我们的损失函数为:

$\sum_{(i, j) : c(i, j)=1}( r^{i,j} - \mu - b^i - b^j - {\mathbf{w}^i}^T \mathbf{x}^j)^2 + \lambda ( {||{\mathbf{w}^i}||}^2 + {||\mathbf{x}^j||}^2 + {b^i}^2 + {b^j}^2 )$

直接用梯度下降我们就能求出所有的 $w, x, b$ .

后来前雅虎研究院的Yehuda Koren还做过许多改进, 有兴趣的可以参考他的论文.

5 练习题

请用上面各种方预测 User 3 对 Item 2 的评分.