欠拟合与过拟合

前面我们已经讲了二个线性模型–感知机和线性回归–和一个广义线性模型, 逻辑回归. 再回顾一下我们学习模型参数采用的步骤: 先定义损失函数, 然后极小化损失函数的策略学习得到模型参数. 用来学习的数据是我们已经收集到的训练数据. 拿线性回归举例, 损失函数:

$L(\mathbf{w}) = \frac {1}{m} \sum_{i=1}^m (h_{\mathbf{w}}(\mathbf{x}^i) - y^i)^2$

然后极小化上式得到 $\mathbf{w}$ , 那么是不是这样求得的 $\mathbf{w}$ 就是最好的呢? 我们先来看一个例子. 下图是由 $sin(2 \pi x)$ (绿色的曲线)生成的一些点(一共10个点), 然后加了一些随机误差.

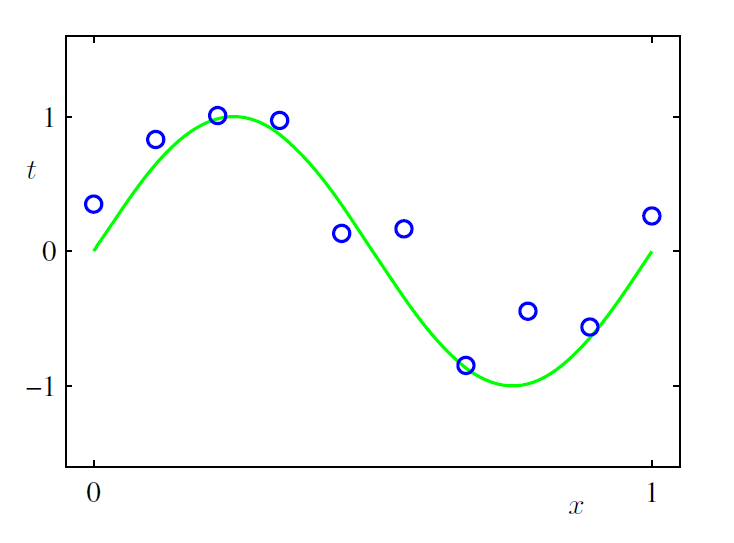
我们的目标是找到一条跟绿色曲线差不多的线, 让那些点尽量分布在这条线周围. 尝试用线性模型来解决这个问题, 前面讲到, 线性模型的假设空间是特征空间里的所有超平面, 而特征往往可以越加越多, 于是:

用0个特征得到一个假设:

$h_{\mathbf{w}}^0 (x) = w_0$

用1个特征( $x$ )得到一个假设:

$h_{\mathbf{w}}^1 (x) = w_0 + w_1 x$

用3个特征( $x,x^2,x^3$ )得到一个假设:

$h_{\mathbf{w}}^3 (x) = w_0 + w_1 x + w_2 x^2 + w_3 x^3$

用9个特征( $x,x^2,\ldots,x^9$ )得到一个假设:

$h_{\mathbf{w}}^9 (x) = w_0 + w_1 x + \ldots + w_9 x^9$

然后我们将这些假设都分别带入上面的损失函数, 然后极小化损失函数求得模型参数.

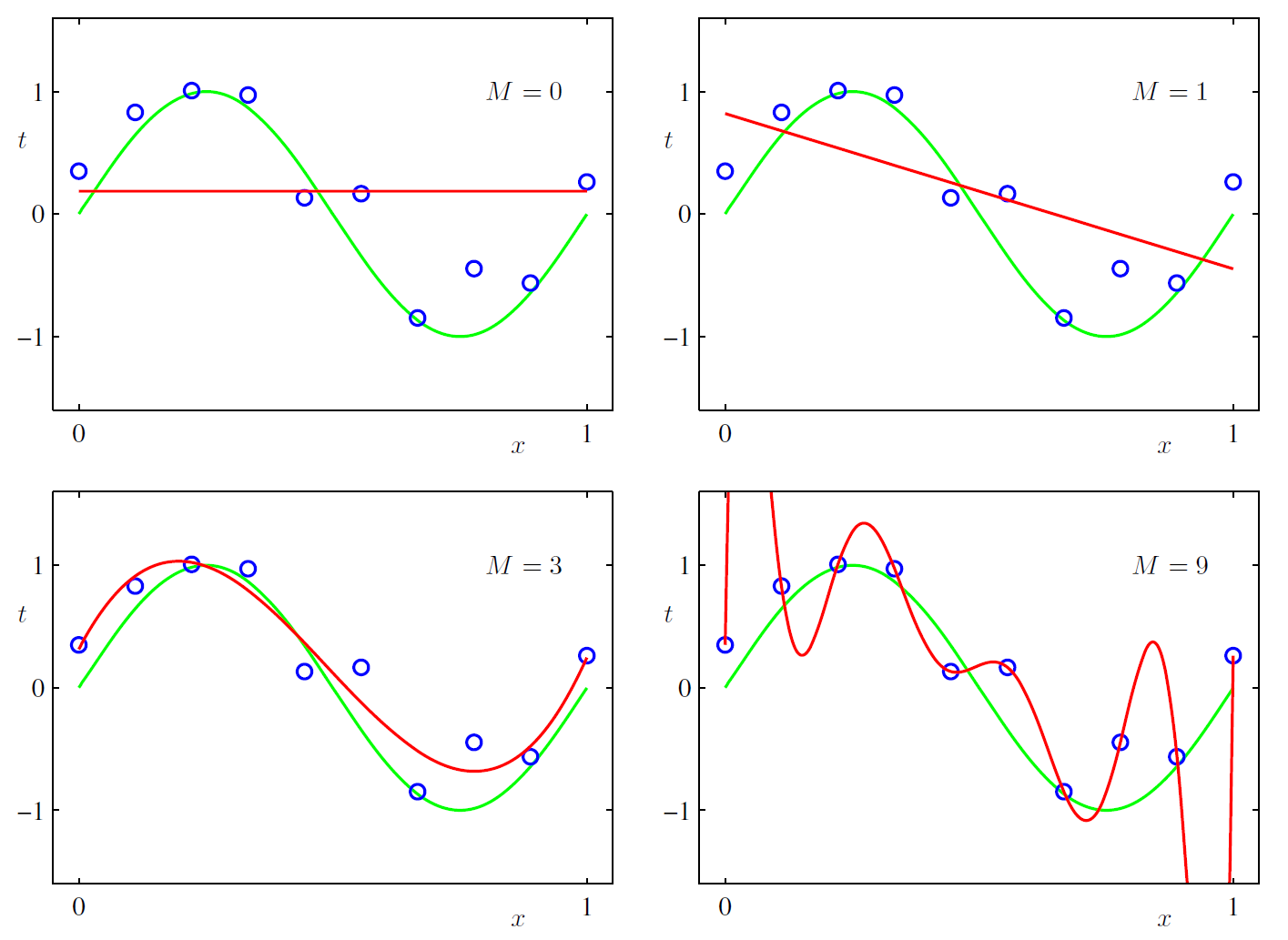
从上面的图形可以看出, 0次方和1次方的曲线似乎差得比较远, 3次的曲线好像刚刚好, 9次方的曲线虽然精确通过了每个点, 但给人的感觉是特别不稳定. 如果我们还有一些测试数据(测试数据也是由 $sin(2\pi x)$ 加随机误差生成)的话, 9次方曲线的表现会很差. 0次方和1次方的曲线在训练数据上表现得就不怎么好, 差得很远, 这种现象叫欠拟合, 或者High bias. 9次方曲线在训练数据上表现很好, 误差为0, 但模型太复杂, 参数过多, 在测试数据上表现会很差, 这种现象叫过拟合, 或者High variance. 我们的目标是在欠拟合和过拟合之间找到一个各方面都很均衡的曲线.

如果”真”模型存在的话, 那么怎么样才能选出一个跟”真”模型很接近的模型呢? 为此我们引入一个概念— 经验风险(或者叫经验损失): 模型 $h(\mathbf{x})$ 关于训练数据集的平均损失称为经验风险(empirical risk)或者经验损失(empirical loss), 记为 $R_{emp}$ :

$R_{emp}(h(\mathbf{x})) = \frac {1}{m} \sum_{i=1}^{m} L(h(\mathbf{\mathbf{x}^i}), y^i)$

我们前面讲到的感知机, 线性回归, 逻辑回归都是采用的极小化这个经验风险学习到的模型参数. 正如上图看到的一样, 一味追求经验风险最小很有可能会出现过拟合现象, 为此我们引入另外一个概念: 结构风险(structural risk)

它是在经验风险的基础上加上了表示模型复杂度的正规化项(regularizer)或者惩罚项(penalty term), 其定义为:

$R_{sr} = \frac {1}{m} \sum_{i=1}^{m} L(h(\mathbf{\mathbf{x}^i}), y^i) + \lambda J(h(\mathbf{x}))$

其中 $\lambda$ 是二者之间的平衡系数. 一般模型的复杂度 $J(h(\mathbf{x}))$ 可以取模型参数 $\mathbf{w}$ 的 $L_2$ 或者 $L_1$ 范数.

对上面曲线拟合的例子, 我们取 $L_2$ 范数看看引入了模型复杂度惩罚项之后, 9次方曲线的拟合效果.

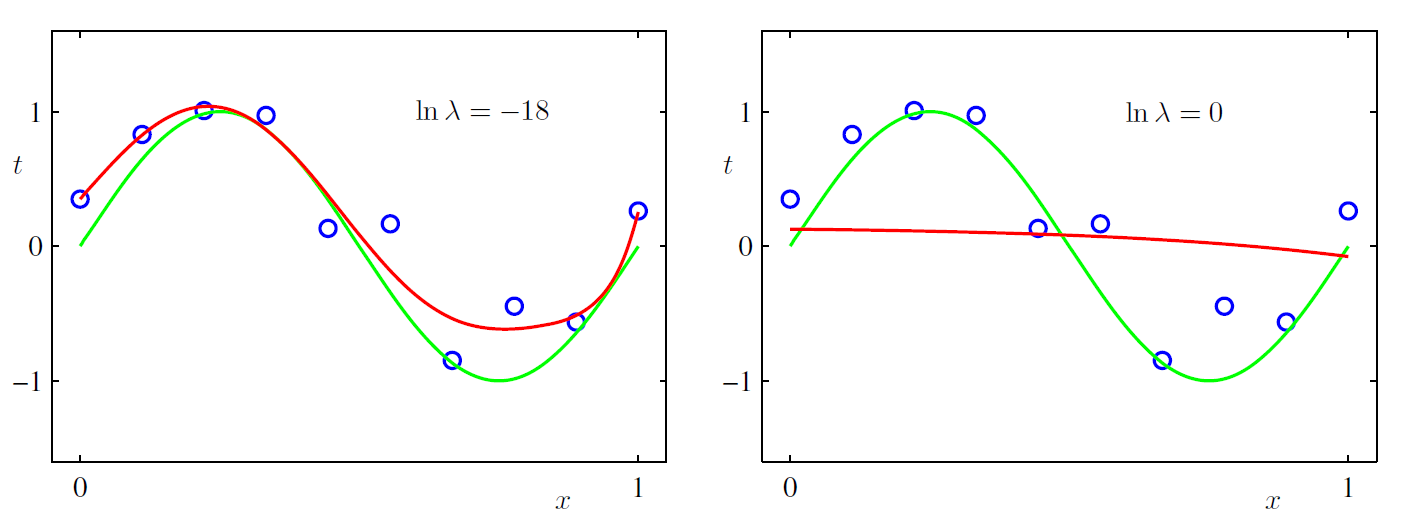
可以看出来, 9次方的曲线也能跟我们真正的绿线比较吻合.

我们再比较一下加入惩罚项前后, $\mathbf{w}$ 参数的大小. 加入惩罚项前:

加入惩罚项后:

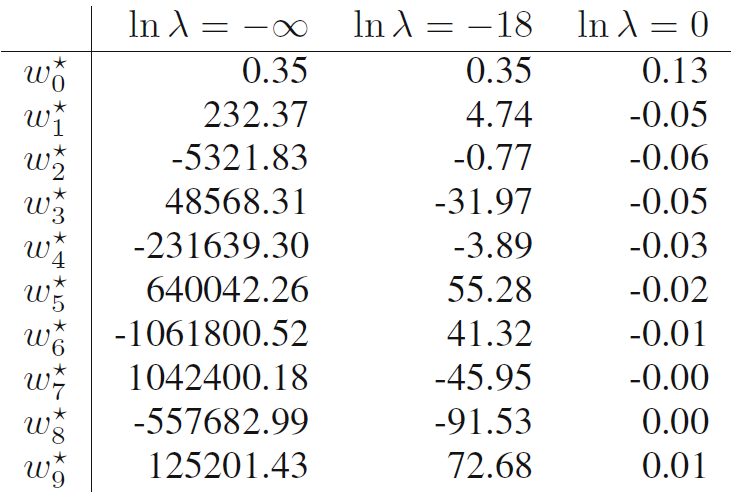
可以看出, 我们对模型复杂度惩罚越大( $\lambda$ 越大), 训练出来的模型会让 $\mathbf{w}$ 越小(曲线越平滑).

参考资料

统计学习方法李航著
Pattern recognization and machine learning