信息论基础

本文主要介绍信息论中常见的一些概念,熵,条件熵,互信息,KL散度.这部分内容非常重要,在很多机器学习模型中都涉及到.

---

1 熵(Entropy)

熵这个概念最初出现在热力学中,1865年由克劳修斯引入,描述在热交换过程中热量与温度的变化. 热力学第一定律告诉我们,热力过程中参与转换与传递的各种能量在数量是守恒的.但它并没有告诉我们,满足能量守恒的过程是否都能实现. 热力学第二定律告诉我们,虽然能量之间可以互相转换,但效率不能达到100%,总有一部分能量会损失掉.

经验告诉我们自然过程都是有方向性的.

• 比如热可以从高温物体自发的,不需付出任何代价地传给温度较低的物体.反之要使热量由低温物体传向高温物体必须付出代价,比如空调.
• 比如高压气体向真空空间膨胀可以自发进行,但相反的压缩过程却不能自发进行,需要外界做功.
• 将一滴墨水滴到清水中,墨水与清水很快就混在一起.把两种不同的气体放在一起,两种气体就自动混合在一起成为混合气体.

熵其实就是”无序化”程度的度量.系统越”有序”,熵越小,系统越”无序”,熵越大.引入熵的概念以后,热力学第二定律的一个等价表述就是孤立系统的一切实际过程都是朝着熵增加的方向进行.上面所列的三个自然过程都遵循了这个道理.

那么信息学中借用熵这个概念来描述什么呢?我们先来看一个例子: 假设有5枚硬币,编号分别为1,2,3,4,5.其中有一个硬币是假的,比其他的要轻,给你一个天平,问最少要使用天平几次才能保证找出假硬币. 稍微想一下,就知道是 2 次.

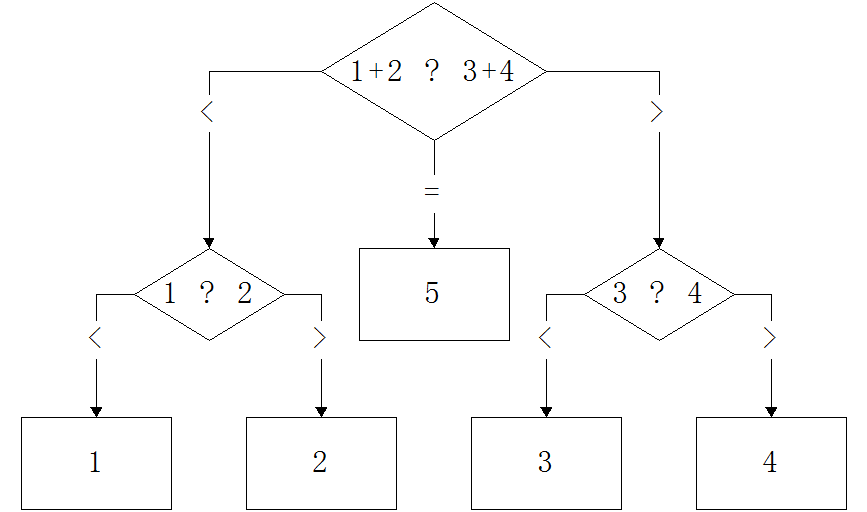
假设$x$是假币的序号,$x \in X = \lbrace 1,2,3,4,5 \rbrace$,一共有5种可能性. 假设$y_i$是第$i$次使用天平得到的结果,$y_i \in Y=\lbrace >,<,= \rbrace$,一共有3种可能性. 使用天平$n$次,获得的结果是$y_1,y_2,\ldots,y_n$,一共有$3^n$种情况. 我们要通过$y_1,y_2,\ldots,y_n$找出$x$,所以每个$y_1,y_2,\ldots,y_n$最多只有一个对应的$x$,于是:

$$3^n \geq 5,n=1.46$$

更进一步分析: 问题等价于设计一套编码$y_1,y_2,\ldots,y_n$来表达$x$,即$x \to y_1,y_2,\ldots,y_n$. $X$的”不确定度”是: $H(X) = \log |X| = \log 5$. $Y$的”表达能力”或者信息量是: $H(Y) = \log |Y| = \log 3$. 至少需要多少个$Y$才能准确表达$X$:

$$n = \frac {H(X)} {H(Y)} = \frac {\log 5} {\log 3} = 1.46$$

为什么要用$\log$来表示”不确定度”或者”表达能力”呢? 如果有人告诉你在某场重要比赛中中国足球队输给了德国队,你可能觉得这件事没什么信息量,因为中国队输球是件高概率的事情.但如果有人告诉你,中国足球队赢了,你的反应肯定不一样,因为这是个小概率事件.中国队赢了德国队这件事就比中国队输给德国队这件事信息量要大,信息量跟概率相关.也就中国队输球这个事件 $x$ 的信息量 $h(x)$ 跟中国队输球的概率 $p(x)$ 相关,但具体是什么关系不知道.如果同时也有一场美国队和葡萄牙队的比赛(跟中国队和德国队的比赛没有任何关系),我们记美国队赢球这个事件记为 $y$.如果事件 $x$ 和 $y$ 一起发生,很显然他们的信息量应该是两个事件的信息量之和,即 $h(x,y)=h(x) + h(y)$.而对这两个独立事件来说有$p(x,y) = p(x)p(y)$,综合这两个式子,马上就能得出 $h(x)$ 和 $p(x)$ 是 $\log$ 之间的关系,即 $h(x) = -\log p(x)$,负号是为了让结果大于0.取 2 为底叫比特,取 $e$ 为底叫奈特,取 10 为底叫哈特. 熵就是这些信息量的平均值.如果中国队有0.1的概率能赢德国队,0.9的概率输给德国队,则中国队和德国队比赛结果的熵为:

$$H(X) = -0.1 \log 0.1 - 0.9 \log 0.9$$

写成数学表达式就是:

$$H(x) = - \sum_x p(x) \log_2 p(x)$$

对连续变量,将求和换成积分即可.

$$H(x) = - \int p(x) \log p(x) dx$$

再来看一个别的例子: 如果我们有个随机变量$X$有8个状态,每个状态的取值都有 1/8 的可能性,我们只需要 3 个bit就能表示这些状态值.用熵的公式计算一下:

$$H(X) = - 8 \times \frac {1}{8} \log \frac {1}{8} = 3$$

如果这8个状态(用$a,b,c,d,e,f,g,h$表示)的概率不相等,假设分别是1/2,1/4,1/8,1/16,1/64,1/64,1/64,1/64,那么平均我们需要几个bit才能表示X呢? 还记得数据结构里的Huffman编码吗?用Huffman编码表示就是0,10,110,1110,111100,111101,111110,111111, 平均长度为:

$$\frac 12 \times 1 + \frac 14 \times 2 + \frac 18 \times 3 + \frac {1}{16} \times 4 + \frac {1}{64} \times 6 \times 4 = 2$$

用熵的公式计算一下:

$$H(X) = -\frac 12 \log \frac 12 - \cdots - 4 \times \frac {1}{64} \log \frac {1}{64} = 2$$

又一次说明了熵就是最短编码的长度.

熵的性质

• 熵只与 $X$ 的分布有关,和$X$ 的取值无关.
• 熵满足不等式 $0 \leq H(X) \leq \log \|X\|$

第二条性质后面的那个等号只有在 $X$ 是均匀分布时成立.也就是说均匀分布的熵最大. 当$X$是伯努利分布时,即$P(X=1)=p,P(X=0)=1-p$,此时$H(X) = -p \log p - (1-p) \log (1-p)$,画成图就是下面的曲线:

可以看出,当$p=0.5$时,熵是最大的.$p=0,1$时,熵为0.

对于事件 $x$,没发生时熵反映的是不确定性,发生以后反映的是信息量.

2 联合熵(Joint Entropy)

两个随机变量X,Y有联合概率分布$p(x,y)$,则表达式:

$$H(X,Y) = -\sum_{x,y} p(x,y) \log p(x,y)$$

称为$X$和$Y$的联合熵.

3 条件熵(Conditional Entropy)

假设我们有联合概率分布 $p(x,y)$,如果 $x$已经知道,那么表达 $y$ 额外所需要的信息是 $-\log p(y\|x)$ ,所以额外所需要的平均信息为:

$$H(Y|X) = -\sum_{x,y} p(x,y) \log p(y|x)$$

利用概率的乘法规则,很容易得到:

$$\begin{equation*} \begin{split} H(X,Y) &= -\sum_{x,y} p(x,y) \log p(x,y) \\ &= -\sum_{x,y} p(x,y) \log {p(x)p(y|x)} \\ &= -\sum_{x,y} p(x,y) \log p(y|x) - \sum_{x,y} p(x,y) \log p(x) \\ &= H(Y|X) - \sum_x p(x) \log p(x) \\ &= H(Y|X) + H(X) \end{split} \end{equation*}$$

同理有:

$$H(X,Y) = H(Y) + H(X|Y)$$

用来描述 $X,Y$ 需要的信息量等于描述$X$的信息量加上给定$X$后描述$Y$所需的信息量.

熵和条件熵的计算很关键,很多机器学习的模型都会用到.下面举个例子.$X$代表学生的专业,$Y$代表是否喜欢电子游戏.如果知道了学生的专业,能预测他是否喜欢电子游戏吗?

X	Y
Math	Yes
History	No
CS	Yes
Math	No
Math	No
CS	Yes
History	No
Math	Yes

求出联合概率分布(Joint Probability)和边缘分布(Marginal Probability).

X,Y	Yes	No
Math	0.25	0.25	P(X=Math)=0.5
CS	0.25	0	P(X=CS)=0.25
History	0	0.25	P(X=History)=0.25
	P(Y=Yes)=0.5	P(Y=No)=0.5	1

$X$ 的熵为:

$$H(X) = -0.5 \log 0.5 - 0.25 \log 0.25 - 0.25 \log 0.25 = 1.5$$

$Y$ 的熵为:

$$H(Y) = -0.5 \log 0.5 - 0.5 \log 0.5 = 1$$

给定某个具体的$X$之后,$Y$的熵为:

$$\begin{equation*} \begin{split} H(Y|X=Math) &= -\sum p(Y|X=Math) \log p(Y|X=Math) \\ &= -p(Y=yes|X=Math)\log p(Y=Yes|X=Math) - p(Y=No|X=Math) \log p(Y=No|X=Math) \\ &= -0.5 \log 0.5 - 0.5 \log 0.5 \\ &= 1 \end{split} \end{equation*}$$

同理计算出

$$H(Y|X=CS) = 0, H(Y|X=History)=0$$

列成表格为:

v	p(X=v)	H(Y;X=v)
Math	0.5	1
History	0.25	0
CS	0.25	0

所以:

$$\begin{equation*} \begin{split} H(Y|X) &= \sum_v p(X=v) H(Y|X=v) \\ &= 0.5 \times 1 + 0.25 \times 0 + 0.25 \times 0 \\ &= 0.5 \end{split} \end{equation*}$$

更详细的计算请参考这个slides.

思考一下: 如果还有个Feature $Z$,比如学生的成绩,通过计算得出 $H(Y\|Z)=0.05$ ,相比专业这个Feature,哪个更有效呢?

4 KL散度(Kullback-leibler Divergence)

考虑有一个不知道的概率分布 $p(x)$,前面我们已经知道了熵是表示$X$编码的最小长度,描述$X$所需要的信息量. 假如我们想用另外一个分布 $q(x)$ 来近似地估计 $p(x)$,那么平均额外多出来的信息量为:

$$\begin{equation*} \begin{split} KL(p||q) &= -\sum p(x) \log q(x) - (-\sum p(x) \log p(x)) \\ &= - \sum p(x) \log {\frac {q(x)} {p(x)}} \end{split} \end{equation*}$$

这个多出来的信息就叫 Kullback-leibler divergence,简称KL散度.

注意 $KL(p||q) \neq KL(q||p)$

可以证明KL散度一定是大于等于0的,当且仅当 $p(x) = q(x)$ 时等于0.KL散度反映的两个概率分布差得到底有多远,或者说他们到底有多接近. 证明KL散度大于0的过程需要用到用Jensen’s Inequality,这里不多说.

5 互信息(Mutual Information)

对于联合分布 $p(x, y)$,如果$x,y$相互独立时,有$p(x,y) = p(x)p(y)$.如果$x,y$不相互独立时,我们可以考虑到底$p(x)p(y)$跟$p(x, y)$差得有多远.

$$\begin{equation*} \begin{split} I(X, Y) &= KL(p(x, y) || p(x)p(y)) \\ &= -\sum p(x, y) \log {\frac {p(x)p(y)} {p(x, y)}} \end{split} \end{equation*}$$

上面这个式子就是 $X,Y$之间的互信息.根据KL散度的性质,互信息也是大于等于0的,当且仅当 $x,y$相互独立时才等于0.也就是说互信息可以反映两个变量之间的相关性,越相关互信息越大.可以利用这点帮助我们选择Feature.

$$\begin{equation*} \begin{split} I(X, Y) &= -\sum p(x, y) \log {\frac {p(x)p(y)} {p(x, y)}} \\ &= -\sum p(x, y) \log {\frac {p(x)}{p(x|y)}} \\ &= H(X) - H(X|Y) \end{split} \end{equation*}$$

同理有:

$$I(X, Y) = H(Y) - H(Y|X)$$

前面说到,熵其实就是随机变量的不确定性.所以互信息反映的也是给定某个条件以后,随机变量的不确定性减少的程度.选择Feature的时候,就要选择那些使不确定性减少最大的Feature.

6 练习题

1. 证明 $0 \leq H(X) \leq \log \| X \|$ ,可以用Jensen’s Inequality或者拉格朗日乘子法.
2. 假设有5个硬币,编号分别是1,2,3,4,5,其中有一个是假的,比其他的硬币轻.已知第一个硬币是假币的概率为1/3,第二个硬币是假币的概率是1/3,剩下三个假币的概率都是1/9.给你一个天平,问平均需要使用天平多少次才能找到假币.

7 参考资料

1. 工程热力学 清华大学出版社
2. 最大熵模型与自然语言处理 c-liu01@mails.tsinghua.edu.cn 的ppt,忘记哪里下载的了.
3. Pattern recognization and machine learning
4. http://www.ruanyifeng.com/blog/2013/04/entropy.html

---