本文主要介绍如何用Map-Reduce的框架处理大矩阵乘法.
1 例子
假设有如下矩阵
其中是一个的矩阵,是一个的矩阵,是一个的矩阵(3维列向量).
很容易计算出:
其中是一个矩阵(4维列向量). 是一个矩阵,矩阵里每一个元素由的第行与的第列求内积得到.
2 矩阵的存储
对一个的矩阵,我们可以用一个的数组来存储,但很显然这不是一个优雅的存储方式. 由于实际工程中我们遇到的矩阵往往都很大,行和列都有上千万或者上亿的规模,而且里面有很多元素都为0,是一个非常稀疏的矩阵. 这时候采用三元组来存储是一个比较好的方式,表示矩阵的第行第列元素为.
上面例子中的矩阵就可以存储为:
| 1 | 1 | 11 |
| 1 | 2 | 12 |
| 1 | 3 | 13 |
| 2 | 1 | 21 |
| 2 | 2 | 22 |
| 2 | 3 | 23 |
| 3 | 1 | 31 |
| 3 | 2 | 32 |
| 3 | 3 | 33 |
| 4 | 1 | 41 |
| 4 | 2 | 42 |
| 4 | 3 | 43 |
3 分块矩阵
实际工程中,矩阵往往很庞大,处理起来不太方便. 在处理大矩阵时,常常把大矩阵视为若干个小矩阵组成. 将矩阵用众线和横线分成若干个小块,每一小块称为的子快,分为子快的矩阵叫分块矩阵.
以下是几种不同构造分块矩阵的方法.
3.1 按列划分
3.2 按行划分
3.3 按行列划分
下面讨论分块矩阵的运算.
3.4 加法
设和是同型矩阵,采用相同的划分方法分块,成为:
其中子块和都是同型矩阵,则与相加只需将他们对应的子块相加.
3.5 转置
3.6 乘法
其中: 是 矩阵,是 矩阵. 是 矩阵,是 矩阵.
注意: 为了乘法可行,要求的列划分与的行划分一致,以保证各个子块间的乘法也可行. 至于的行划分和的列划分没有限制.
于是
其中:
4 矩阵-向量乘法
4.1 算法一
假设有一个的矩阵,其中第行第列的元素为. 假设有一个维向量,其中第个元素为. 于是矩阵和向量的乘积结果是一个维向量,其中第个元素为:
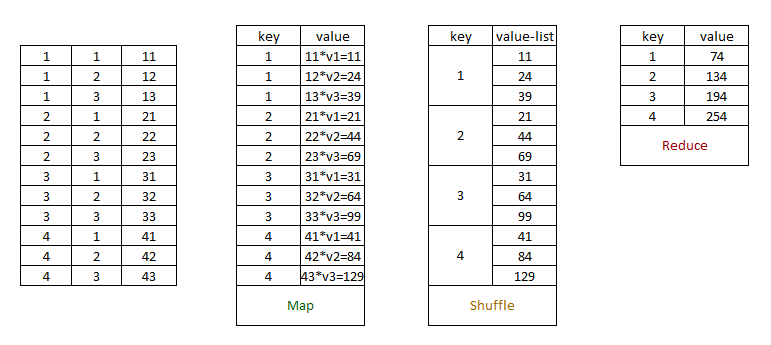
如果不算太大,向量可以直接放到内存里面,这时候我们采用Map-Reduce的框架来计算的话,Map函数和Reduce函数可以这么设计:
Map函数: 每个Map任务将整个向量和矩阵的一个文件块作为输入. 对每个矩阵元素,Map任务会产生一个键值对
Reduce函数: Reduce任务将所有与给定键值关联的值求和即可得到
图示如下:
4.2 算法二
在实际工程中,向量的维度往往特别大,有上亿,甚至百亿的规模,内存里根本放不下,这时候我们求需要将矩阵和向量分块. 这时候可以将他们做合适的列划分和行划分. 为了乘法可行,同样需要保证矩阵的列划分和向量的行划分一致,如下图所示:
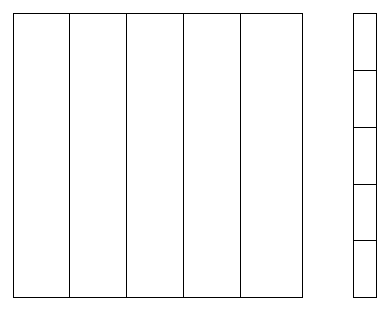
假设矩阵的每个子块和向量的每个子块都可以放进内存(内存还放不下的话可以做更细的划分),这时候就可以用前面提到的分块矩阵的乘法,然后采用Map-Reduce的计算框架计算.
5 矩阵-矩阵乘法
矩阵与矩阵的乘法比矩阵与向量的乘法稍微复杂一点,但跟矩阵与向量的乘法思路也类似,都是从矩阵-矩阵乘法的定义入手,仔细观察,一步一步拆成Map-Reduce的框架. 矩阵与矩阵的乘法可以只用一个Map-Reduce实现, 也可以用两个Map-Reduce实现.
假设是一个矩阵,是一个矩阵,则是一个矩阵.
5.1 单步Map-Reduce
很显然,的各个元素的计算都是独立的,这就是为并行化创造了条件.
-
计算时,我们需要把第一行的元素都找出来,把第一列的元素都找出来,两者对应相乘再求和.
-
计算时,我们需要把第一行的元素都找出来,把第二列的元素都找出来,两者对应相乘再求和.
-
……
-
计算时,我们需要把第一行的元素都找出来,把第r列的元素都找出来,两者对应相乘再求和.
-
计算时,我们需要把第二行的元素都找出来,把第一列的元素都找出来,两者对应相乘再求和.
-
……
-
计算时,我们需要把第m行的元素都找出来,把第一列的元素都找出来,两者对应相乘再求和.
对里的元素来说,计算 的时候都要用到,对的元素来说,计算 的时候都要用到. 所有我们考虑在Map阶段,把的每个元素都存成个键值对,把里的每个元素都存成个键值对.
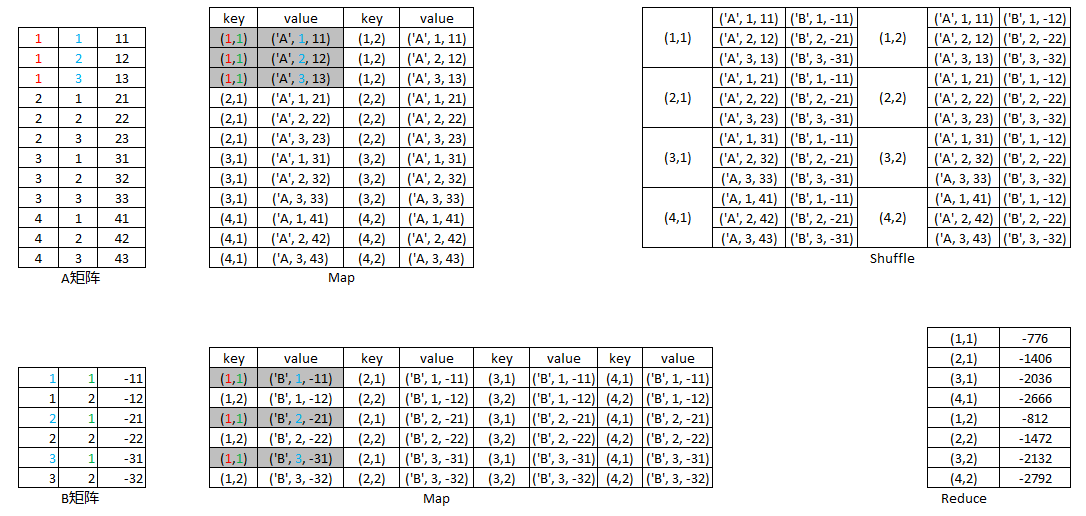
Map函数: 把任意拆成个key,value对,对应矩阵的元素下标,其中,,标示这条记录来自矩阵. 把任意拆成个key,value对,对应矩阵的元素下标,其中,,标示这条记录来自矩阵.
Reduce函数: 把对应的value列表按照分别来自和来自做内积即可.
图示如下:
5.2 两步Map-Reduce
//TODO
5.3 Map-Reduce加分块矩阵
有了前面矩阵-矩阵乘法1的Map-Reduce实现和上面分块矩阵的知识,在处理大矩阵时,只需要把矩阵分好块,在每个块上的操作都是一个小矩阵乘法问题,最后把小矩阵的乘积再汇总即可.
6 参考资料
- http://blog.csdn.net/xyilu/article/details/9066973
- http://www.mmds.org/#ver21
- 线性代数与解析几何 清华大学出版社